Regresyon denklemi

Bir fenomen veya süreç çalışırken, çok fazlagenellikle faktörler (değişkenler) ile cevap fonksiyonu (bağımlı miktar) arasında bir ilişki olup olmadığını ve etkileşimlerinin ne kadar yakın olduğunu bulmak gereklidir. Bunu yapmak için, çeşitli aşamalarda gerçekleştirilen regresyon analizine izin verilir.

Regresyon analizinin ana aşamalarından biriFaktörler ve yanıt fonksiyonu arasındaki matematiksel ilişkinin hesaplanması, bunlar arasındaki ilişkiyi nicelleştirmenizi sağlar. Bu bağımlılığa regresyon denklemi denir. Formal olarak, en küçük kareler yöntemi, belirtilen denklemin belirlenmesi için temel analitik yöntem olarak kabul edilir, çünkü bu yöntem optimaldir ve korelasyon alanının noktalarını yumuşatmaya izin verir. Bununla birlikte, pratikte böyle bir işlevi bulmak oldukça zordur, çünkü çalışılan fenomen, bu bilimsel alandaki seleflerimizin tecrübesi hakkında ya da “deneme-yanılma” yöntemiyle, çeşitli işlevlerin basit bir araştırmasını ve değerlendirmesini yapmak için teorik bilgiye dayanmak zorundayız. Eğer başarılı olursa, çeşitli faktörlerin etki fonksiyonu üzerindeki etkisinin yeterince değerlendirilmesine olanak veren bir regresyon denklemi elde edilir, yani, faktörlerin belirli değerleri (bağımlı değişkenler) için yanıt fonksiyonunun (bağımlı değişken) beklenen değerini bulmaktır.

Regresyon için başlangıç ​​verilerianaliz, faktör x'in değerlerini ve çalışmanın deneysel kısmında elde edilen cevap fonksiyonunun (Y) karşılık gelen değerini kullanır. Açıklık ve daha rahat algı için, bu değerler tablo biçiminde sunulur.

Doğrusal regresyon denklemi, bir kural olarak,aşağıdaki form Y = a + b ∙ X. Bir sabit katsayısı (sabit) a ve değişken faktör X'un değeri ile çarpılan bir regresyon katsayısı (eğim) b içerir. Katsayı b, faktör değeri bir birim tarafından değiştirildiğinde, yanıt fonksiyonundaki ortalama değişikliği gösterir. Katsayıyı (b) kullanarak regresyon denklem grafiğini çizerken, çizginin apsis hattına eğimi de belirlenebilir. Bu katsayı belirli özelliklere sahip olduğuna dikkat edilmelidir:

· B farklı değerler alabilir;

· B simetrik degildir, yani, Y'nin X üzerindeki etkisini incelerken degerini degistirir;

· Korelasyon katsayısının ölçüm birimi, cevap fonksiyonu Y'nin ölçü biriminin X değişkenlerinin ölçüm birimine oranıdır;

· X ve Y değişkenlerinin ölçü birimleri değişirse, regresyon katsayısının değeri de değişir.

Çoğu durumda, gözlenen değerler nadirdirtam olarak düz bir çizgide bulunur. Pratikte, tahmin edilen değerleri oluşturduğum regresyon hattında belirli bir deneysel veri dağılımını gözlemlemek her zaman mümkündür. Bireysel bir noktanın regresyon çizgisinden teorik veya tahmin edilen değerinden sapması geri kalanı olarak adlandırılır.

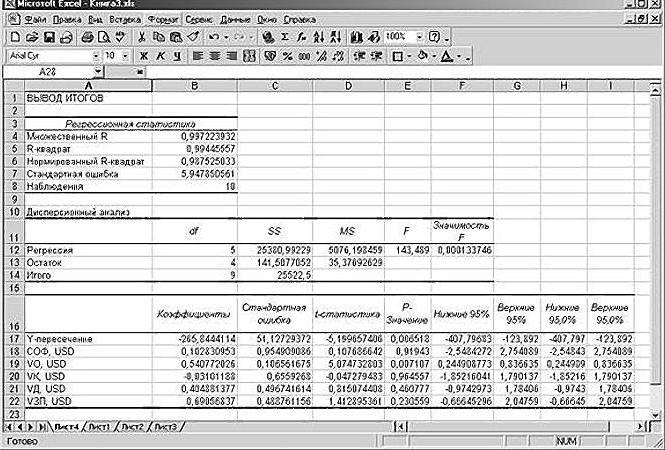
Çok sık pratikte, örnekregresyon denklemi, en küçük kareler yöntemi olan katsayıların değerlerini hesaplamanın ana yöntemi. Katsayılar, değişken faktörün ve cevap fonksiyonunun değerlerinin örneğini temsil eden ilk verilerden hesaplanır.

İlk bakışta hesaplama gibi görünebilirregresyon denkleminde katsayıların değerleri oldukça karmaşık ve zaman alıcıdır. Ama bu öyle değil. Bu denkleme dahil bütün faktörleri hesaplamak için değişkenler ve bağımlı değişkenler arasındaki ilişkinin derecesini belirlemek mümkün olacak, ama grafiksel formda elde değerleri temsil kalmayacak ham verilere göre, araştırmacılar, sayısız yazılım paketleri (en kolay olan Microsoft Excel) sunmaktadır.